第1回 音楽は宇宙とつながっている!? ——沖野成紀
これから東海大学教養学部芸術学科の教員たちによる、音楽の不思議に関する連載が始まります。さて、まずは連載のタイトルである「世界は音楽でできている」って、一体どういうことだろうと思った人も多いでしょう。例えば、「世界は音楽で満ちている」という表現であれば意味が分かりますよね。ちょっと荒唐無稽な話に聞こえるかもしれませんが、音楽についての「考え方」の歴史を紐解いていけば、「世界が音楽でできている」ということの意味を理解してもらえるのではないかと思います。
中世ヨーロッパの公用語であったラテン語で「音楽」に相当する言葉は「ムシカ(musica)」です。その響きから、なんとなく英語の「ミュージック(music)」の語源だということが分かりますよね。でも、ムシカには、ミュージックよりもはるかに広い意味が与えられていました。例えば、後世に大きな影響を及ぼした6世紀の学者ボエティウスは、3種類のムシカ、すなわちムシカ・ムンダーナ(musica mundana. 直訳すれば「世界の音楽」)とムシカ・フマーナ(musica humana. 同「人間の音楽」)、ムシカ・インストルメンタリス(musica instrumentalis. 同「器官の音楽」)について語っています。
3番目のムシカは、英語に直訳すればインストルメンタル・ミュージックとなるので器楽のことかと思うかもしれませんが、実は「人工器官」(つまり楽器)のみならず、「自然器官」(つまり声帯)から発せられる声楽も、ムシカ・インストルメンタリスに含まれると今日考えられています。つまり、私たちのいう普通の意味での「音楽」は、全てムシカ・インストルメンタリスに含まれます。
これに対して、ムシカ・ムンダーナとは、例えば天体の運行、四大元素の調和、季節の移り替わりなどを指します。これを大宇宙の調和とすれば、小宇宙としての人間の調和がムシカ・フマーナです。つまり、決して声とかではなく、魂内の調和、魂と身体間の調和、身体各部間の調和を意味したのです。それらはいずれも音として聞こえることすらできません。
では、なぜそれらがムシカと呼ばれたのでしょうか。「宇宙や人間の音楽」と聞くと、今の私たちにはとても奇異な感じがしますね。でも、先ほどのように「調和」と抽象的に書かれていると、そこに引っかかる人はほとんどいないのではないかと思います。
ところで、「調和」とは英語でいうとどの単語に相当するか分かりますか。そう、「ハーモニー(harmony)」ですね。ハーモニーは今日の音楽用語としては「和声」と訳されますが、当時の音楽にはまだ今のような和声はありませんでした。その代わりに、当時の「ハーモニー」という言葉には、今も残る重要な意味がありました。特に形容詞形で「ハーモニック(harmonic)」というときには、1、1/2、 1/3、 1/4 、……という数列などを指していました。これは今でも「ハーモニック・シーケンス」と呼ばれ、日本語では「調和数列」と訳されました。つまり、調和といっても決して抽象的で曖昧なことではなく、それは数秩序に裏打ちされたハーモニーだったのです。
音楽は理系科目だった
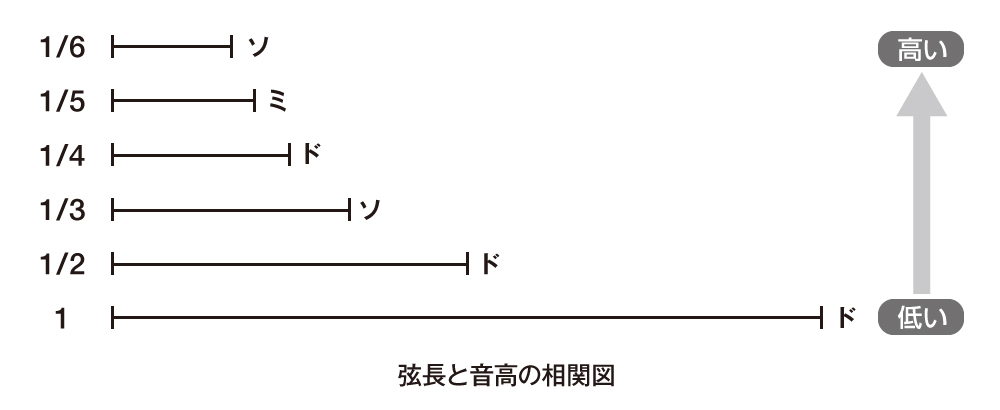
音楽において調和数列のもつ意義は重要です。弦楽器で開放弦(※)の長さを1とすると、1/2、1/3、……という数列は、指などで押さえることで弦の長さを半分、三分の一の長さにすることを意味します。すると、それらの弦の発する音は、開放弦の音をドとすると、1/2はオクターヴ上のド、1/3はその上のソ、1/4はその上のド(最初のドの2オクターヴ上)、1/5はさらにその上のミの音になります。
※開放弦 ギターなどの弦楽器で、指で弦を押さえずにそのまま弾いたときに鳴る音。楽器の基本の音。
そして、17世紀になると、これらの音は、弦の長さを変えなくても、最初の開放弦のドの音の中に全て「倍音」として含まれていることが発見されました。これも「ハーモニック」です。倍音についてはこの連載で主題として取り上げる日が来ると思いますが、ここでは「倍音」と訳された元の言葉が何であったかということだけにしておきましょう。
さらに驚くべきことに、これら調和数列において隣り合う音を同時に鳴らした場合、少なくとも最初のいくつかの組み合わせでは、うなりが全くないという意味で「純正な」協和音程が得られます。1と1/2で8度(オクターヴのこと)、1/2と1/3で5度、1/3と1/4で4度、1/4と1/5で長3度……というように。
そうして、これらの数比から様々な音律も作られました。音律とは、ドレミファ……の各音の高さの厳密な決め方のことです。今では十二平均律という、1オクターヴを12の均等な半音に分割する音律が一般的ですが、歴史上いろいろな音律が考案されてきました。その中でも最も古いとされるピタゴラス音律を紹介しましょう。
ピタゴラス音律では、上に挙げた協和音程比のうち、最初の2つだけを使います。すなわち、1 : 1/2=2 : 1の8度と1/2 : 1/3=3 : 2の5度です。弦長が2 : 1つまり半分になると、8度(オクターヴ)上の音になります。弦長が3 : 2つまり2/3になると、5度上の音になります。
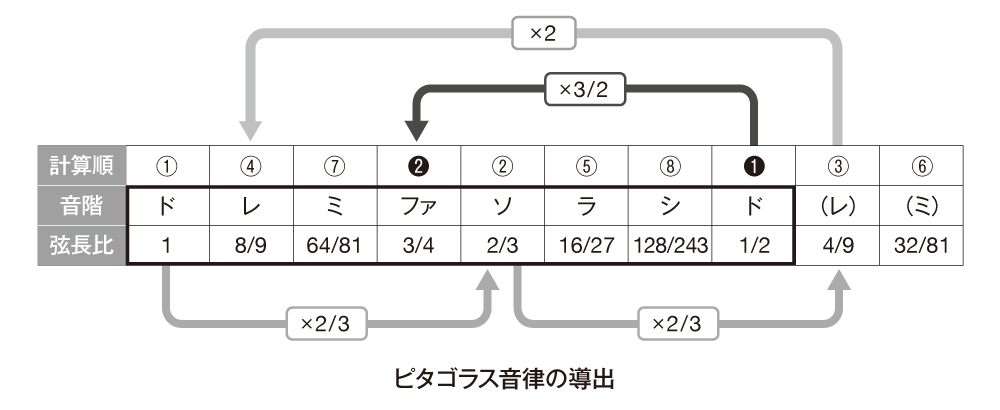
では、5度上とはどういうことでしょうか? 音楽理論において音程を表す度数は、差ではなくて、数え年のように最初の音も1として数えるので、ドの5度上は、ドを1として5番目の音、つまりソということになります。ソの弦長を更に2/3にすると更にその5度上、すなわちオクターヴ上のレ(4/9)が決まります。これを2倍してオクターヴ下げてやれば、最初のドの次のレ(8/9)が求まります。
この操作を繰り返すことで、ド→ソ→レ→ラ→ミ→シ→ファ♯→……と順に各音の比が求まり、逆方向に計算すると(弦長を3/2倍にすると5度下の音になる)、ド→ファ→シ♭→……と順に求まっていきます。
いかがでしょう。数比としてのハーモニーが、どれほど、音程や音律、倍音や協和といった音楽の基礎を形作っているか、その一端でも実感していただけたでしょうか。ちなみに、中世の大学の教養課程では、標準的な理系科目として、数学・幾何・天文学と並んでムシカがあったのですが、そこでは作曲や演奏ではなく、数比や数列や級数といった数学的技法が重視され、学ばれていたそうです。
ここまで読み進めて、「ムシカ・インストルメンタリスと数比との関係は分かったけれど、ムンダーナやフマーナとの関係は?」と、思った人がいるかもしれません。そう、3種類のムシカを提唱したボエティウスも、実はムンダーナやフマーナについては漠然とした抽象論を手短に語るのみで、具体的な計算などは試みていません。
天体と音楽の関係
まさに中世が終わろうとする時、しかも一般には中世の暗黒を追い払ったと見なされている近代的自然科学の祖の一人、ヨハネス・ケプラーその人によって、皮肉にも天体の音楽は緻密に計算されることになるのです。1619年に出版された『世界のハーモニー』において、ケプラーは詳細な観測データに基づき周到な計算をしました。その結果、ついに各天体の角速度(※)の変化の比を音高の変化の比に変換し、それを楽譜にして世に示しました。
※角速度 回転運動において単位時間あたりに物体が進む角度を表す物理量のこと。

(上段左から、土星、木星、火星、地球。下段左から、金星、水星、月)
ここに、本来耳に聞こえないはずのムシカ・ムンダーナは、ムシカ・インストルメンタリスと共通の秩序である数比を介して、耳に聞こえるムシカとして示されたのです。ネットを検索すれば楽譜と演奏例を数多見聞きできると思いますが、中でもお薦めは、実際の惑星の公転通りにグリッサンド(※)で音高変化させているWillie Ruffらの試みです。彼の名と〝The Harmony of the World〟で検索してみてください。また、有名なホルストの組曲《惑星》をはじめとして、ヨーロッパにはこのテーマに沿った音楽作品もたくさんあります。ただしケプラーが計算した宇宙の音楽をどれほど反映しているのかは分かりませんが……。
※グリッサンド 一音一音の音高を区切ることなく、滑るように移行させる演奏技法のこと
ちょっと難しかったかもしれませんが、「世界は音楽でできている」のタイトルが示す意味をお分かりいただけたのではないでしょうか。それは、「世界は数比でできている」「世界の根底には数秩序がある」と言い換えても構いません。でも、そう言い換えてしまうと、今の自然科学的な観点から見れば、逆に当たり前のことと思われてしまうかもしれません。
すなわち、様々なレベルで物理には数の秩序があって、それが数式で表されるのは当然であり、その中にたまたま協和音程の比が見出されたとしても、それは単なる偶然の一致である、と。でも、それくらいのことで、「世界は……」って言い過ぎでは?
しかし、現代物理学は、単に数が根底にあるということ以上のことを、その数で表現される秩序のあり方に音楽と宇宙の間で共通点があることを、見出しました。「1/f ゆらぎ」がそれです。次回は、生物に心地よさを与えるとも言われる「1/f ゆらぎ」について考えてみましょう。

おきの・しげき 1960年兵庫県生まれ。東京大学基礎科学科卒業、同大学院人文科学研究科博士課程満退。1996年、東海大学教養学部芸術学科に赴任。専門は哲学的音楽美学から実験音楽美学へとシフト。論文はインターネット上で閲覧可。著書に『古楽の音律』(共訳。春秋社)、『人はなぜ音楽を聴くのか』(共訳。東海大学出版会)など。
バックナンバー